Análisis detallado del circuito de la serie RC
2024-05-08
20469
El circuito de la serie RC, que consiste en una resistencia y un condensador, sirve como un componente fundamental en diseños de sistemas electrónicos básicos y avanzados.Ayuda a comprender los principios clave, como la respuesta de frecuencia, el cambio de fase y el filtrado de señal, que juegan un papel importante en el diseño de circuitos y el procesamiento de señales.Esta exploración cubre los conceptos básicos teóricos y se extiende a aplicaciones prácticas a través de experimentos y simulaciones.Al ensamblar físicamente el circuito o modelarlo digitalmente, los alumnos pueden comprender visualmente el proceso de carga y los efectos de los iones del componente V ariat, lo que hace que los conceptos complejos sean más accesibles y memorables.
Catalogar
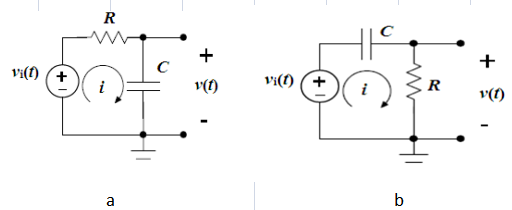
Figura 1: Diferentes voltajes de salida de los circuitos RC
Introducción al circuito RC
Un circuito RC, abreviatura de un circuito de capacidad de resistencia, es fundamental en la electrónica para manipular señales a través de resistencias y condensadores.Estos circuitos son particularmente conocidos por su capacidad para cambiar las fases y las señales de filtro, utilizando arreglos simples de estos componentes.Un circuito RC básico, a menudo denominado circuito RC de primer orden, generalmente incluye solo una resistencia y un condensador.
En una configuración típica, el voltaje de entrada se aplica a la disposición en serie de una resistencia y un condensador.La salida se puede dibujar a través de la resistencia o el condensador, cada una dando diferentes respuestas a las frecuencias de señal debido a las características únicas del condensador.Esta versatilidad permite que los circuitos RC desempeñen una variedad de roles en dispositivos electrónicos, como señales de acoplamiento y filtrado o incluso para convertir formas de onda cuando se someten a un voltaje de paso.
El circuito RC se puede configurar de varias maneras: series, paralelos o una combinación de ambos, conocidos como series-paralelo.Cada configuración afecta las frecuencias de señal de manera diferente: las conexiones en serie tienden a atenuar frecuencias bajas, mientras que las conexiones paralelas se utilizan para amortiguar las frecuencias más altas.Esta diferencia se debe principalmente a la forma en que las resistencias y condensadores interactúan con el circuito;Las resistencias se oponen directamente a la corriente, mientras que los condensadores la almacenan y la liberan, impactando cómo el circuito responde a diferentes frecuencias.
A diferencia de los circuitos que incluyen inductores, como los circuitos LC, los circuitos RC simples no pueden resonar ya que las resistencias no almacenan energía.Este atributo influye claramente en cómo se utilizan los circuitos RC, centrándose en su capacidad para filtrar en lugar del almacenamiento de energía o resonancia.Cada configuración tiene un propósito específico, lo que hace que las herramientas versátiles de los circuitos RC tanto en el estudio teórico como en la aplicación práctica en diseño electrónico.
Circuito de la serie RC
Un circuito de la serie RC, esencialmente compuesto por una resistencia (Riñonal) y un condensador (do) En serie, opera con un principio directo.Cuando se cierra el interruptor del circuito, el condensador comienza a cargarse desde el voltaje aplicado (V), iniciando un flujo de corriente a través del circuito.A medida que el condensador se carga, la corriente aumenta gradualmente hasta que el condensador alcanza su capacidad, momento en el cual deja de aceptar la carga, y la corriente se estabiliza en su valor máximo, calculado como 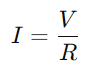 .
.
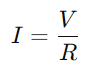 .
.El proceso de carga del condensador puede describirse matemáticamente por la ecuación 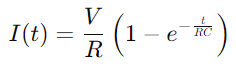 , donde yo es la corriente, V es el voltaje, Riñonal es la resistencia, do es la capacitancia, T es el tiempo y mi es la base del logaritmo natural.Esta fórmula refleja cómo la corriente cambia con el tiempo a medida que el condensador carga, con el producto de los valores de resistencia y capacitancia (RC) que definen la constante de tiempo del circuito, indicativo de la velocidad a la que se carga el condensador.
, donde yo es la corriente, V es el voltaje, Riñonal es la resistencia, do es la capacitancia, T es el tiempo y mi es la base del logaritmo natural.Esta fórmula refleja cómo la corriente cambia con el tiempo a medida que el condensador carga, con el producto de los valores de resistencia y capacitancia (RC) que definen la constante de tiempo del circuito, indicativo de la velocidad a la que se carga el condensador.
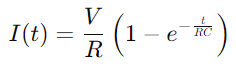 , donde yo es la corriente, V es el voltaje, Riñonal es la resistencia, do es la capacitancia, T es el tiempo y mi es la base del logaritmo natural.Esta fórmula refleja cómo la corriente cambia con el tiempo a medida que el condensador carga, con el producto de los valores de resistencia y capacitancia (RC) que definen la constante de tiempo del circuito, indicativo de la velocidad a la que se carga el condensador.
, donde yo es la corriente, V es el voltaje, Riñonal es la resistencia, do es la capacitancia, T es el tiempo y mi es la base del logaritmo natural.Esta fórmula refleja cómo la corriente cambia con el tiempo a medida que el condensador carga, con el producto de los valores de resistencia y capacitancia (RC) que definen la constante de tiempo del circuito, indicativo de la velocidad a la que se carga el condensador.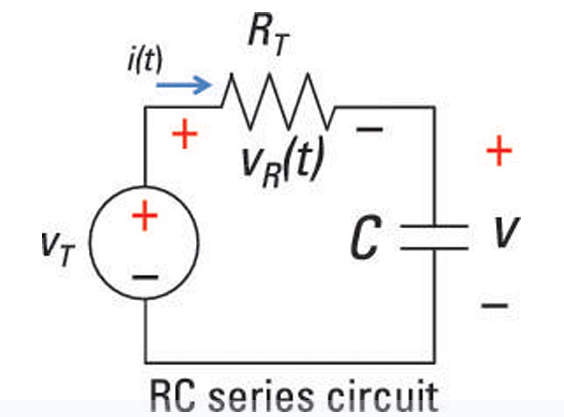
Figura 2: circuito de la serie RC
La descarga ocurre cuando se abre el interruptor, invirtiendo el proceso: se libera la energía almacenada en el condensador, lo que hace que la corriente fluya en la dirección opuesta hasta que el condensador esté drenado.Este ciclo de carga y descarga es crucial en aplicaciones como la conversión de señal, el filtrado y los circuitos de tiempo debido a la manera predecible en que cambian la corriente y el voltaje.
Figura 3: cortocircuito de la serie RC
El comportamiento del circuito de la serie RC también varía con la frecuencia.A bajas frecuencias, el condensador actúa más como un circuito abierto, lo que impide en gran medida el flujo de corriente.A medida que aumenta la frecuencia, la reactancia capacitiva disminuye, lo que facilita la transferencia de la corriente.Este cambio en la impedancia con frecuencia permite que el circuito de la serie RC actúe como un filtro, atenuando selectivamente frecuencias por debajo de un cierto umbral (frecuencia de giro 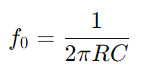 ).
).
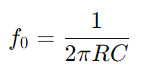 ).
).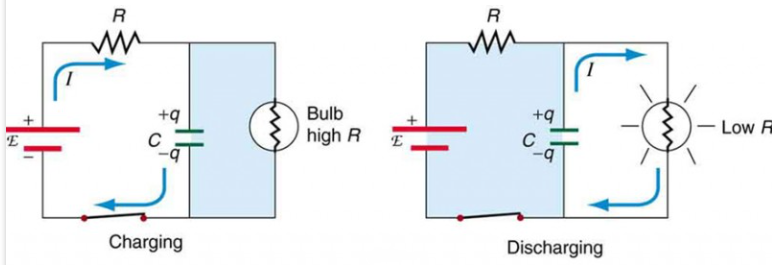
Figura 4: Carga y descarga de circuitos de la serie RC
Además de las operaciones de estado estacionario, los circuitos RC también se estudian para sus respuestas transitorias cuando se someten a cambios repentinos en el voltaje, como cuando una fuente de alimentación de CC se enciende o desactiva.Este escenario se denomina un proceso transitorio, donde el circuito pasa de un estado estable a otro.La dinámica de este proceso depende significativamente de la constante de tiempo RC, que rige la rapidez con que el circuito reacciona a los cambios.
En última instancia, los circuitos de la serie RC cumplen múltiples funciones en aplicaciones de CC y CA, manejando tareas que van desde las señales de retraso hasta la integración o el acoplamiento de varios elementos del circuito.Esta versatilidad proviene de las interacciones únicas entre la resistencia y el condensador, que en conjunto determinan la respuesta general del circuito a cambios en el voltaje y la frecuencia.
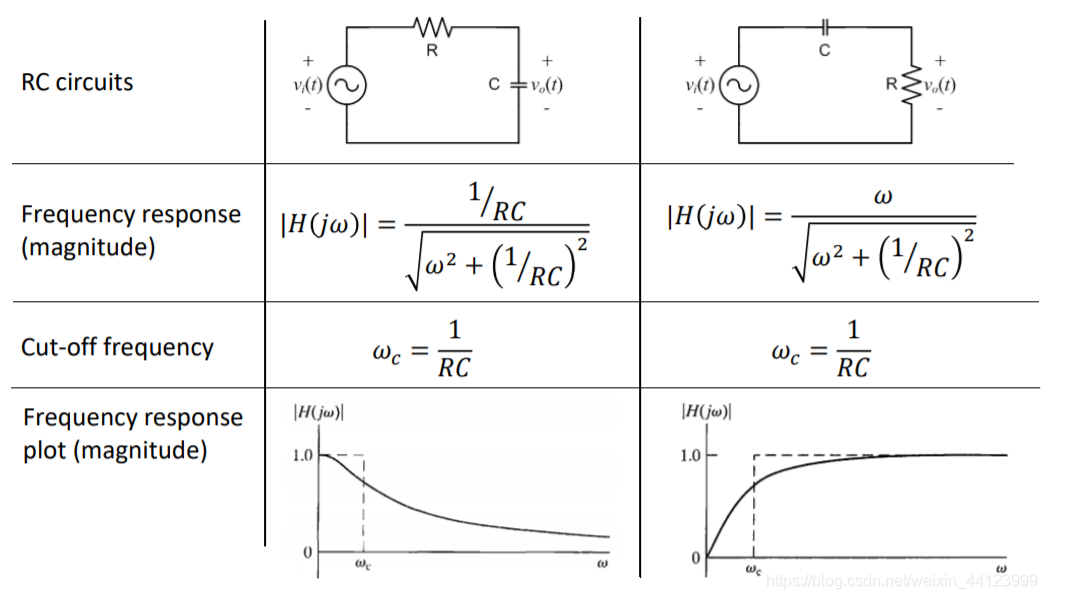
Figura 5: Diagrama de circuito de la serie RC y fórmula de frecuencia
En un circuito de la serie RC, la interacción entre la resistencia (R) y el condensador (DO) influye tanto en el flujo de corriente como de la distribución de voltaje.El papel principal de la resistencia es regular el flujo de corriente.Esta relación se cuantifica por la ley de Ohm, que establece 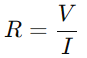 , dónde V es voltaje y I es actual.Esencialmente, la resistencia actúa como un cuello de botella, controlando cuánta electricidad puede pasar en un momento dado.
, dónde V es voltaje y I es actual.Esencialmente, la resistencia actúa como un cuello de botella, controlando cuánta electricidad puede pasar en un momento dado.
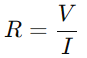 , dónde V es voltaje y I es actual.Esencialmente, la resistencia actúa como un cuello de botella, controlando cuánta electricidad puede pasar en un momento dado.
, dónde V es voltaje y I es actual.Esencialmente, la resistencia actúa como un cuello de botella, controlando cuánta electricidad puede pasar en un momento dado.La función del condensador es ligeramente más intrincada, ya que almacena temporalmente la energía eléctrica y luego la libera nuevamente en el circuito.El voltaje a través del condensador (VC) se correlaciona con su carga almacenada (Q) y se calcula usando la fórmula 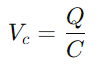 .Esta relación destaca la capacidad del condensador para retener la carga, impactando directamente el voltaje que exhibe.Durante la operación, la dinámica de cargar y descargar el condensador es vital para comprender los circuitos de RC.La constante de tiempo (τ), definido como
.Esta relación destaca la capacidad del condensador para retener la carga, impactando directamente el voltaje que exhibe.Durante la operación, la dinámica de cargar y descargar el condensador es vital para comprender los circuitos de RC.La constante de tiempo (τ), definido como 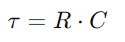 , mide qué tan rápido el condensador alcanza aproximadamente el 63.2% del voltaje completo suministrado por la fuente (V0).Esta constante de tiempo es indicativa de cómo el circuito se adapta a los cambios de entrada, con las propiedades de resistencia y condensador que dictan el ritmo de estos ajustes.
, mide qué tan rápido el condensador alcanza aproximadamente el 63.2% del voltaje completo suministrado por la fuente (V0).Esta constante de tiempo es indicativa de cómo el circuito se adapta a los cambios de entrada, con las propiedades de resistencia y condensador que dictan el ritmo de estos ajustes.
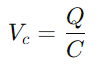 .Esta relación destaca la capacidad del condensador para retener la carga, impactando directamente el voltaje que exhibe.Durante la operación, la dinámica de cargar y descargar el condensador es vital para comprender los circuitos de RC.La constante de tiempo (τ), definido como
.Esta relación destaca la capacidad del condensador para retener la carga, impactando directamente el voltaje que exhibe.Durante la operación, la dinámica de cargar y descargar el condensador es vital para comprender los circuitos de RC.La constante de tiempo (τ), definido como 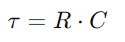 , mide qué tan rápido el condensador alcanza aproximadamente el 63.2% del voltaje completo suministrado por la fuente (V0).Esta constante de tiempo es indicativa de cómo el circuito se adapta a los cambios de entrada, con las propiedades de resistencia y condensador que dictan el ritmo de estos ajustes.
, mide qué tan rápido el condensador alcanza aproximadamente el 63.2% del voltaje completo suministrado por la fuente (V0).Esta constante de tiempo es indicativa de cómo el circuito se adapta a los cambios de entrada, con las propiedades de resistencia y condensador que dictan el ritmo de estos ajustes.El voltaje a través del condensador en cualquier momento dado durante la carga está dada por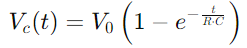 , ilustrando un aumento no lineal a medida que se llena el condensador.Esta ecuación describe cómo la tasa de carga se ralentiza a medida que el condensador se acerca a la capacidad total.
, ilustrando un aumento no lineal a medida que se llena el condensador.Esta ecuación describe cómo la tasa de carga se ralentiza a medida que el condensador se acerca a la capacidad total.
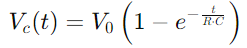 , ilustrando un aumento no lineal a medida que se llena el condensador.Esta ecuación describe cómo la tasa de carga se ralentiza a medida que el condensador se acerca a la capacidad total.
, ilustrando un aumento no lineal a medida que se llena el condensador.Esta ecuación describe cómo la tasa de carga se ralentiza a medida que el condensador se acerca a la capacidad total.Por el contrario, durante la descarga, el voltaje del condensador disminuye según 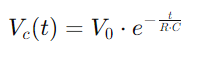 , retratando una disminución lineal en la energía almacenada con el tiempo.Este proceso proporciona una imagen clara de cómo se libera la energía del condensador en el circuito.En aplicaciones de CA, la diferencia de fase entre el voltaje y la corriente, φ, se vuelve crítico.Esta diferencia, calculada como
, retratando una disminución lineal en la energía almacenada con el tiempo.Este proceso proporciona una imagen clara de cómo se libera la energía del condensador en el circuito.En aplicaciones de CA, la diferencia de fase entre el voltaje y la corriente, φ, se vuelve crítico.Esta diferencia, calculada como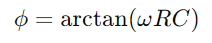 dónde Ω representa la frecuencia angular, muestra el retraso causado por el condensador, que afecta el momento entre cuando los flujos de corriente y el voltaje cambian en los componentes.
dónde Ω representa la frecuencia angular, muestra el retraso causado por el condensador, que afecta el momento entre cuando los flujos de corriente y el voltaje cambian en los componentes.
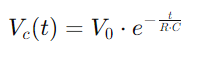 , retratando una disminución lineal en la energía almacenada con el tiempo.Este proceso proporciona una imagen clara de cómo se libera la energía del condensador en el circuito.En aplicaciones de CA, la diferencia de fase entre el voltaje y la corriente, φ, se vuelve crítico.Esta diferencia, calculada como
, retratando una disminución lineal en la energía almacenada con el tiempo.Este proceso proporciona una imagen clara de cómo se libera la energía del condensador en el circuito.En aplicaciones de CA, la diferencia de fase entre el voltaje y la corriente, φ, se vuelve crítico.Esta diferencia, calculada como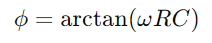 dónde Ω representa la frecuencia angular, muestra el retraso causado por el condensador, que afecta el momento entre cuando los flujos de corriente y el voltaje cambian en los componentes.
dónde Ω representa la frecuencia angular, muestra el retraso causado por el condensador, que afecta el momento entre cuando los flujos de corriente y el voltaje cambian en los componentes.En general, la resistencia limita y dirige el flujo de corriente mientras el condensador almacena y modula el voltaje.Juntos, determinan las características de respuesta del circuito, como la rapidez con que puede cargar y descargar y los cambios de fase que ocurren en escenarios de corriente alternos.Este comportamiento combinado respalda las operaciones fundamentales de los circuitos de la serie RC, lo que los hace integrales en varias aplicaciones electrónicas.
Ecuaciones básicas del circuito de la serie RC
Para comprender el comportamiento de un circuito de la serie RC, es crucial comenzar con las ecuaciones básicas que describen su respuesta a los cambios en el voltaje de entrada.Suponga que tenemos un voltaje de entrada cambiante representado como Vin (t), con el voltaje a través de la resistencia marcado como VR (t) y a través del condensador como VC (t).En un circuito de la serie, la misma corriente, Él) fluye a través de la resistencia y el condensador.
Aplicando la Ley de Voltaje de Kirchhoff (KVL), que establece que el voltaje total alrededor de cualquier circuito cerrado en un circuito debe igual a cero, encontramos que el voltaje de entrada es igual a la suma de los voltajes a través de la resistencia y el condensador:
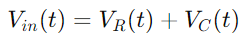
El voltaje a través de la resistencia se puede calcular utilizando la ley de Ohm:
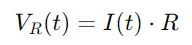
Para el condensador, el voltaje VC (t) está relacionado con la carga Q (t) que tiene, dada por:
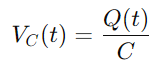
Dado que la corriente se define como la tasa de flujo de carga, tenemos:
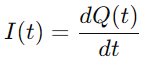
Sustituyendo P (t) en la ecuación para VC (t), y usando la derivada de carga Él), derivamos la ecuación diferencial de núcleo para el circuito de la serie RC:
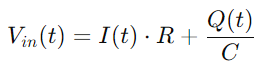
Reemplazando aún más P (t) con la integral de Él), obtenemos:
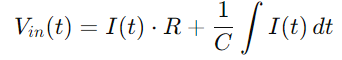
Para la corriente I (t), considerando la tasa de cambio de voltaje en todo el condensador, usamos:
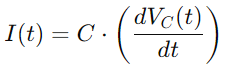
La integración de todas estas relaciones nos da la ecuación diferencial que describe el voltaje a través del condensador:
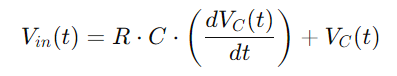
Esta es una ecuación diferencial lineal de primer orden que captura el cambio de voltaje dependiente del tiempo a través del condensador.Resolver esta ecuación nos permite describir con precisión cómo evoluciona el voltaje del condensador.Esta comprensión es fundamental para analizar los ciclos de carga y descarga del condensador, así como la respuesta del circuito a diferentes frecuencias.Este enfoque integral proporciona una visión profunda de las características dinámicas del circuito de la serie RC.
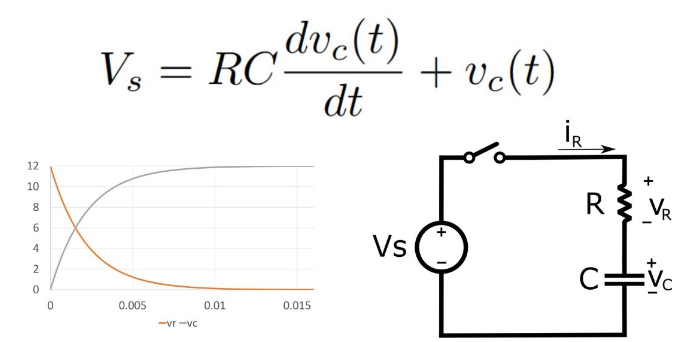
Figura 6: Ecuación diferencial de voltaje
Impedancia del circuito de la serie RC
Para reescribir la descripción de un circuito de la serie RC, con un enfoque en la interacción humana y una explicación directa y simplificada, mejoremos las experiencias tangibles y las operaciones paso a paso involucradas mientras mantienen el mensaje central y la coherencia:
En un circuito de la serie RC, la resistencia y el condensador trabajan en conjunto para controlar el flujo de electricidad, crucial cuando se trata de corrientes alternativas.La impedancia total del circuito, representada como  , combina la resistencia R y la reactancia capacitiva XC.La característica clave de esta configuración es que los valores de impedancia para ambos componentes varían con los cambios de frecuencia.A medida que aumenta la frecuencia, la impedancia del condensador disminuye, lo que permite pasar más corriente, mientras que la resistencia esencialmente permanece constante.
, combina la resistencia R y la reactancia capacitiva XC.La característica clave de esta configuración es que los valores de impedancia para ambos componentes varían con los cambios de frecuencia.A medida que aumenta la frecuencia, la impedancia del condensador disminuye, lo que permite pasar más corriente, mientras que la resistencia esencialmente permanece constante.
 , combina la resistencia R y la reactancia capacitiva XC.La característica clave de esta configuración es que los valores de impedancia para ambos componentes varían con los cambios de frecuencia.A medida que aumenta la frecuencia, la impedancia del condensador disminuye, lo que permite pasar más corriente, mientras que la resistencia esencialmente permanece constante.
, combina la resistencia R y la reactancia capacitiva XC.La característica clave de esta configuración es que los valores de impedancia para ambos componentes varían con los cambios de frecuencia.A medida que aumenta la frecuencia, la impedancia del condensador disminuye, lo que permite pasar más corriente, mientras que la resistencia esencialmente permanece constante.La impedancia, denotada como Z y medido en ohmios (Ω), juega un papel fundamental en la determinación de cómo reacciona el circuito a la corriente alterna.Como en los circuitos de la serie RL, la resistencia Riñonal y reactancia capacitiva xdo de un circuito RC forman un triángulo conocido como el triángulo de impedancia.Este triángulo se relaciona estrechamente con el triángulo de voltaje, y al aplicar el teorema de Pitagorean, puede calcular la impedancia total del circuito.
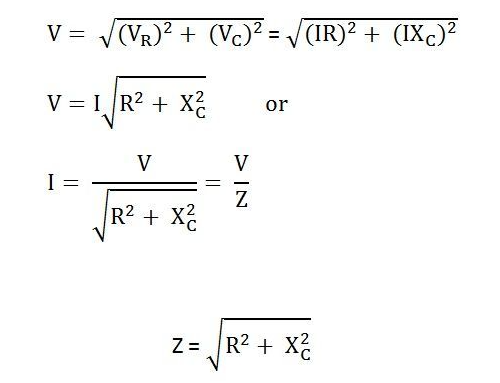
Figura 7: Fórmula de cálculo del circuito de la serie RC
Cuando se trata de aplicaciones prácticas, considere auriculares, que usan estos principios.Los auriculares de alta impedancia, a menudo superiores a 200 ohmios, se usan típicamente con computadoras de escritorio, amplificadores de potencia y equipos de audio profesionales.Estos modelos de alta impedancia coinciden bien con las capacidades de salida de la electrónica de grado profesional.Al usar estos auriculares, es crucial ajustar el volumen gradualmente para evitar sobrecargar y dañar los delicados componentes internos, como la bobina de voz.
Por el contrario, los auriculares de baja impedancia, generalmente por debajo de 50 ohmios, se prefieren para dispositivos portátiles como reproductores de CD, reproductores de MD o reproductores de MP3.Estos auriculares requieren menos energía para ofrecer audio de alta calidad, lo que los hace ideales para uso móvil.Sin embargo, también requieren una atención cuidadosa a los niveles de sensibilidad para garantizar un rendimiento óptimo y evitar daños en los auriculares o la audición.
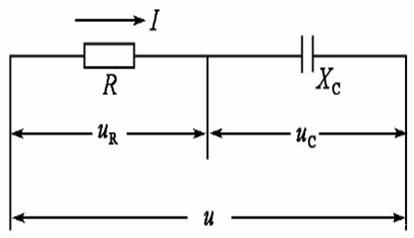
Figura 8: Diagrama de impedancia del circuito de la serie RC
Procedimientos de admisión y análisis de los circuitos de la serie RC
La admisión mide la facilidad con qué facilidad un circuito de la serie RC puede realizar electricidad, calculada como la inversa de la impedancia (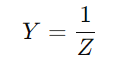 ).Este valor integra tanto la resistencia (Riñonal) y la reactancia (incógnita) del circuito.La resistencia se opone al flujo de corriente al convertir la energía eléctrica en calor, mientras que la reactancia almacena energía temporalmente en el circuito.
).Este valor integra tanto la resistencia (Riñonal) y la reactancia (incógnita) del circuito.La resistencia se opone al flujo de corriente al convertir la energía eléctrica en calor, mientras que la reactancia almacena energía temporalmente en el circuito.
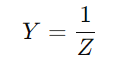 ).Este valor integra tanto la resistencia (Riñonal) y la reactancia (incógnita) del circuito.La resistencia se opone al flujo de corriente al convertir la energía eléctrica en calor, mientras que la reactancia almacena energía temporalmente en el circuito.
).Este valor integra tanto la resistencia (Riñonal) y la reactancia (incógnita) del circuito.La resistencia se opone al flujo de corriente al convertir la energía eléctrica en calor, mientras que la reactancia almacena energía temporalmente en el circuito.Para calcular la admisión
Empiece por escribir la impedancia 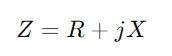 , donde R significa resistencia, incógnita para reactancia, y j es la unidad imaginaria.Use la fórmula y = 1/(Riñonal + + jx).Esta operación involucra números complejos y nos da
, donde R significa resistencia, incógnita para reactancia, y j es la unidad imaginaria.Use la fórmula y = 1/(Riñonal + + jx).Esta operación involucra números complejos y nos da 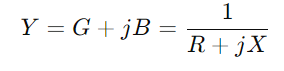 .Aquí, GRAMO es la conductancia (capacidad de flujo de corriente real) y B es la susceptancia (la capacidad del circuito para reaccionar a los cambios en la corriente).
.Aquí, GRAMO es la conductancia (capacidad de flujo de corriente real) y B es la susceptancia (la capacidad del circuito para reaccionar a los cambios en la corriente).
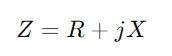 , donde R significa resistencia, incógnita para reactancia, y j es la unidad imaginaria.Use la fórmula y = 1/(Riñonal + + jx).Esta operación involucra números complejos y nos da
, donde R significa resistencia, incógnita para reactancia, y j es la unidad imaginaria.Use la fórmula y = 1/(Riñonal + + jx).Esta operación involucra números complejos y nos da 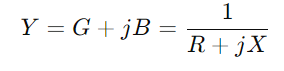 .Aquí, GRAMO es la conductancia (capacidad de flujo de corriente real) y B es la susceptancia (la capacidad del circuito para reaccionar a los cambios en la corriente).
.Aquí, GRAMO es la conductancia (capacidad de flujo de corriente real) y B es la susceptancia (la capacidad del circuito para reaccionar a los cambios en la corriente).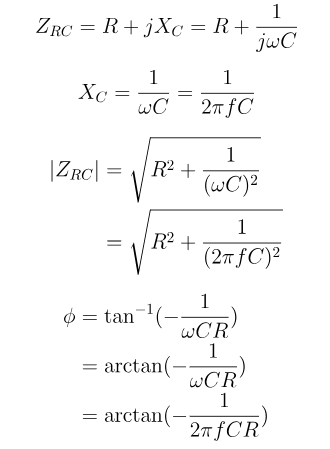
Figura 9: Calculadora de impedancia de circuito RC de serie RC
Este cálculo revela no solo la conductividad del circuito sino también sus características de respuesta dinámica, cruciales para el análisis del circuito de CA.La conductancia y la susceptancia, tomadas en conjunto, indican cómo el circuito pasa la corriente y cómo almacena y libera energía.
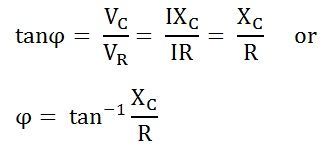
Figura 10: Fórmula de ángulo de fase
Aplicación práctica
Los ingenieros utilizan valores de admisión para mejorar el diseño de circuitos, especialmente en aplicaciones de alta frecuencia, como circuitos de radiofrecuencia.Ajustar la admisión ayuda a la coincidencia de impedancia, la reducción de la reflexión de la señal y el aumento de la eficiencia de la transmisión.
Al estudiar la respuesta de admisión, los ingenieros pueden evaluar y predecir el rendimiento del circuito en diversas condiciones, como respuesta de frecuencia, estabilidad y sensibilidad.Equipe con un osciloscopio y un generador de señal para medir el voltaje y la corriente del circuito a frecuencias variables.Concéntrese especialmente en la frecuencia de corte para probar predicciones teóricas y validarlas contra observaciones prácticas.Para circuitos de CA, comience determinando la reactancia (XC) del condensador con 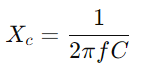 , dónde F es la frecuencia de la señal.Calcular la impedancia total
, dónde F es la frecuencia de la señal.Calcular la impedancia total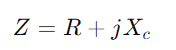 Y luego admitido
Y luego admitido 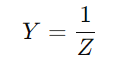 .
.
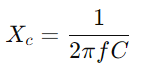 , dónde F es la frecuencia de la señal.Calcular la impedancia total
, dónde F es la frecuencia de la señal.Calcular la impedancia total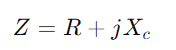 Y luego admitido
Y luego admitido 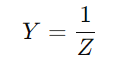 .
.Analizar la diferencia de fase usando 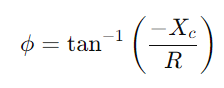 para comprender la alteración de la forma de la señal.Examine cómo el circuito maneja diferentes frecuencias, particularmente observando el comportamiento a la frecuencia de corte
para comprender la alteración de la forma de la señal.Examine cómo el circuito maneja diferentes frecuencias, particularmente observando el comportamiento a la frecuencia de corte 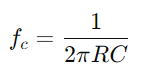 , donde el circuito cambia de pasar a las señales de bloqueo.Evaluar cómo la impedancia y la diferencia de fase varían con la frecuencia es crucial para diseñar filtros y procesadores de señal efectivos.Discuta cómo la selectividad de frecuencia, los cambios de fase y la atenuación de la señal debido a las propiedades del circuito afectan aplicaciones prácticas como el filtrado y el ajuste electrónico.
, donde el circuito cambia de pasar a las señales de bloqueo.Evaluar cómo la impedancia y la diferencia de fase varían con la frecuencia es crucial para diseñar filtros y procesadores de señal efectivos.Discuta cómo la selectividad de frecuencia, los cambios de fase y la atenuación de la señal debido a las propiedades del circuito afectan aplicaciones prácticas como el filtrado y el ajuste electrónico.
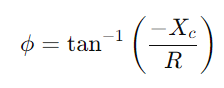 para comprender la alteración de la forma de la señal.Examine cómo el circuito maneja diferentes frecuencias, particularmente observando el comportamiento a la frecuencia de corte
para comprender la alteración de la forma de la señal.Examine cómo el circuito maneja diferentes frecuencias, particularmente observando el comportamiento a la frecuencia de corte 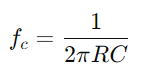 , donde el circuito cambia de pasar a las señales de bloqueo.Evaluar cómo la impedancia y la diferencia de fase varían con la frecuencia es crucial para diseñar filtros y procesadores de señal efectivos.Discuta cómo la selectividad de frecuencia, los cambios de fase y la atenuación de la señal debido a las propiedades del circuito afectan aplicaciones prácticas como el filtrado y el ajuste electrónico.
, donde el circuito cambia de pasar a las señales de bloqueo.Evaluar cómo la impedancia y la diferencia de fase varían con la frecuencia es crucial para diseñar filtros y procesadores de señal efectivos.Discuta cómo la selectividad de frecuencia, los cambios de fase y la atenuación de la señal debido a las propiedades del circuito afectan aplicaciones prácticas como el filtrado y el ajuste electrónico.Este enfoque desglosa los procesos operativos en pasos manejables, enriqueciendo la comprensión del usuario con ideas prácticas sobre el manejo y el análisis de los circuitos de la serie RC.
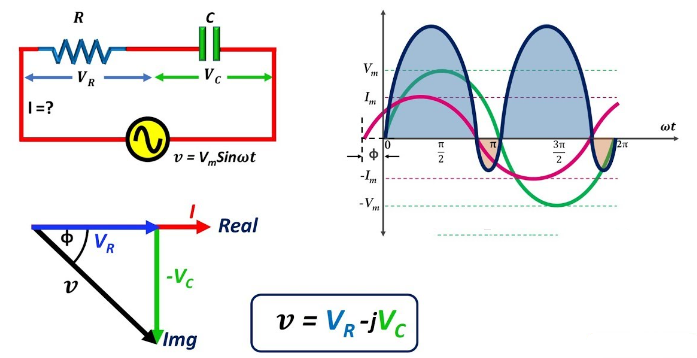
Figura 11: Características de los circuitos de la serie RC
Diagrama de fasor del circuito de la serie RC
En un circuito de la serie RC, todos los elementos comparten la misma corriente debido a la configuración de su serie.Esta corriente uniforme actúa como una línea de base para nuestro diagrama de fasor, que ayuda a visualizar la relación entre diferentes voltajes y corrientes en el circuito.Designemos esta corriente I como el fasor de referencia, colocado a cero grados en el diagrama.En el diagrama, la corriente I se establece horizontalmente a la derecha, estableciendo la línea de referencia de cero grado.El voltaje a través de la resistencia (URiñonal) está en fase con la corriente porque las resistencias no causan ningún cambio de fase.De este modo, URiñonal se dibuja como un vector horizontal en la misma dirección que I, extendiendo desde el origen.
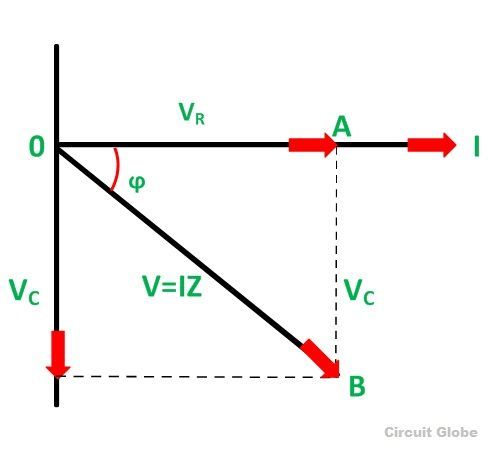
Figura 12: Diagrama de Phasor de la serie RC Serie
En contraste, el voltaje a través del condensador (Udo) conduce la corriente en 90 grados debido a la propiedad capacitiva de retrasar la fase actual.Este voltaje está representado por un vector vertical que apunta hacia arriba, comenzando desde la punta del URiñonal vector.El voltaje total U en el circuito está la suma vectorial de U Rand Udo.Esta suma forma un triángulo recto con URiñonal y Udo como lados adyacentes y opuestos, respectivamente.La hipotenusa de este triángulo, que se extiende desde el origen hasta la punta del Udo vector, representa U.
La corriente sinusoidal a través del circuito viene dada por el pecado (ωt), donde IM es la amplitud de corriente máxima y Ω es la frecuencia angular.En consecuencia, el voltaje a través de la resistencia es 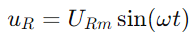 , reflejando la forma de onda actual.El voltaje a través del condensador está dado por
, reflejando la forma de onda actual.El voltaje a través del condensador está dado por 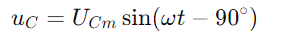 , indicando un cambio de fase de -90 ° (o 90 grados por delante de la corriente).El triángulo derecho del diagrama de fasor aclara que
, indicando un cambio de fase de -90 ° (o 90 grados por delante de la corriente).El triángulo derecho del diagrama de fasor aclara que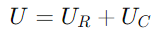 no está solo en magnitud sino también en relación de fase, con el vector de voltaje terminal (U) Completando el triángulo.
no está solo en magnitud sino también en relación de fase, con el vector de voltaje terminal (U) Completando el triángulo.
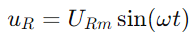 , reflejando la forma de onda actual.El voltaje a través del condensador está dado por
, reflejando la forma de onda actual.El voltaje a través del condensador está dado por 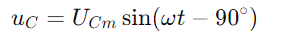 , indicando un cambio de fase de -90 ° (o 90 grados por delante de la corriente).El triángulo derecho del diagrama de fasor aclara que
, indicando un cambio de fase de -90 ° (o 90 grados por delante de la corriente).El triángulo derecho del diagrama de fasor aclara que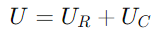 no está solo en magnitud sino también en relación de fase, con el vector de voltaje terminal (U) Completando el triángulo.
no está solo en magnitud sino también en relación de fase, con el vector de voltaje terminal (U) Completando el triángulo.
Figura 13: Diagrama de fasor de voltaje del circuito de la serie RC
Puntos clave en el análisis de los circuitos RC de la serie
Impedancia en el circuito de la serie RC, representada como Z, combina resistencia (Riñonal) y el efecto reactivo de la capacitancia en una sola medida que varía con la frecuencia de la señal.Se expresa matemáticamente como 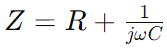 , dónde Ω es la frecuencia angular y do es la capacitancia.Aquí, Riñonal constituye la parte real de la impedancia, y
, dónde Ω es la frecuencia angular y do es la capacitancia.Aquí, Riñonal constituye la parte real de la impedancia, y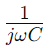 representa la parte imaginaria, lo que indica cómo el condensador influye en el circuito.
representa la parte imaginaria, lo que indica cómo el condensador influye en el circuito.
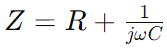 , dónde Ω es la frecuencia angular y do es la capacitancia.Aquí, Riñonal constituye la parte real de la impedancia, y
, dónde Ω es la frecuencia angular y do es la capacitancia.Aquí, Riñonal constituye la parte real de la impedancia, y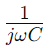 representa la parte imaginaria, lo que indica cómo el condensador influye en el circuito.
representa la parte imaginaria, lo que indica cómo el condensador influye en el circuito.La forma en que los cambios de impedancia con la frecuencia son fundamentales para usar circuitos RC de la serie en aplicaciones de filtrado.A frecuencias más bajas, el circuito exhibe una mayor impedancia, bloqueando efectivamente estas frecuencias.Por el contrario, a frecuencias más altas, la impedancia cae, lo que permite que estas frecuencias pasen más libremente.Este comportamiento hace que la serie RC Circuits sea ideal para tareas como filtrar el ruido no deseado de baja frecuencia o pasar señales de alta frecuencia.
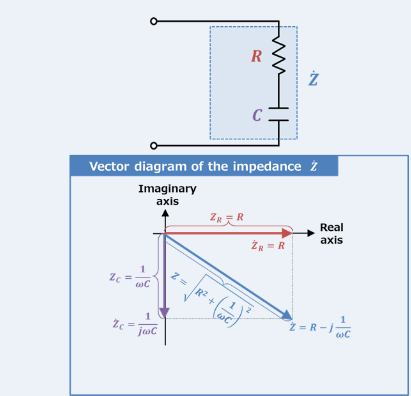
Figura 14: Diagrama de vector de impedancia del circuito de la serie RC
Conclusión
Desde el filtrado de frecuencias no deseadas hasta las respuestas de la señal de conformación, el circuito de la serie RC es fundamental en una amplia gama de funciones electrónicas.Al comprender los principios subyacentes, como la impedancia, las relaciones fasorales y el comportamiento dependiente de la frecuencia de estos circuitos, ingenieros y diseñadores están equipados para soluciones artesanales que manejan efectivamente la integridad de la señal en sistemas electrónicos complejos.El examen detallado de estos circuitos, respaldado por análisis matemáticos y representaciones visuales como diagramas de fasor, ofrece una visión integral que sea importante para cualquier persona que busque profundizar su comprensión de la dinámica electrónica del circuito o mejorar sus habilidades prácticas en el diseño y la solución de problemas de circuitos.
Preguntas frecuentes [Preguntas frecuentes]
1. ¿Cuál es el principio del circuito RC?
El principio de un circuito RC (resistencia y capacitor) gira en torno a los procesos de carga y descarga del condensador a través de la resistencia.En este circuito, la capacidad del condensador para almacenar y liberar energía eléctrica interactúa con la resistencia, que controla la velocidad a la que el condensador carga o descarga.
2. ¿Por qué un circuito RC es una corriente de plomo?
En un circuito RC, la corriente conduce el voltaje a través del condensador porque el condensador debe comenzar a cargarse antes de que su voltaje pueda aumentar.Dado que la corriente fluye hacia el condensador para cargarlo, la corriente alcanza su punto máximo antes de que el voltaje a través del condensador alcance su máximo.Este efecto provoca un cambio de fase en el que la fase de corriente conduce la fase de voltaje hasta 90 grados, dependiendo de la frecuencia de la señal de entrada.
3. ¿Cómo cambia el voltaje en un circuito RC?
El cambio de voltaje en un circuito RC durante la carga se describe mediante una función exponencial.Cuando se aplica un voltaje, el voltaje a través del condensador inicialmente aumenta rápidamente, luego se ralentiza a medida que se acerca al voltaje de suministro.Matemáticamente, esto se expresa como 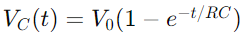 , dónde Vdo(t) es el voltaje a través del condensador en el momento t, V0 es el voltaje de suministro, y RC es la constante de tiempo del circuito, lo que determina qué tan rápido se carga el condensador.Por el contrario, durante la descarga, el voltaje a través del condensador disminuye exponencialmente, después de la ecuación
, dónde Vdo(t) es el voltaje a través del condensador en el momento t, V0 es el voltaje de suministro, y RC es la constante de tiempo del circuito, lo que determina qué tan rápido se carga el condensador.Por el contrario, durante la descarga, el voltaje a través del condensador disminuye exponencialmente, después de la ecuación 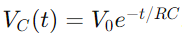 .
.
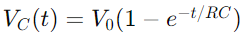 , dónde Vdo(t) es el voltaje a través del condensador en el momento t, V0 es el voltaje de suministro, y RC es la constante de tiempo del circuito, lo que determina qué tan rápido se carga el condensador.Por el contrario, durante la descarga, el voltaje a través del condensador disminuye exponencialmente, después de la ecuación
, dónde Vdo(t) es el voltaje a través del condensador en el momento t, V0 es el voltaje de suministro, y RC es la constante de tiempo del circuito, lo que determina qué tan rápido se carga el condensador.Por el contrario, durante la descarga, el voltaje a través del condensador disminuye exponencialmente, después de la ecuación 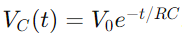 .
. ACERCA DE NOSOTROS
Satisfacción del cliente cada vez.Confianza mutua e intereses comunes.
ACERCA DE NOSOTROS
Satisfacción del cliente cada vez.Confianza mutua e intereses comunes.
prueba de funcionamiento.Los productos más rentables y el mejor servicio es nuestro compromiso eterno.
Artículo caliente
- Son CR2032 y CR2016 intercambiables
- MOSFET: definición, principio de trabajo y selección
- Instalación y prueba de retransmisión, interpretación de los diagramas de cableado de retransmisión
- CR2016 vs. CR2032 ¿Cuál es la diferencia?
- NPN vs. PNP: ¿Cuál es la diferencia?
- ESP32 vs STM32: ¿Qué microcontrolador es mejor para usted?
- LM358 Guía completa del amplificador operacional Dual: Pinuts, diagramas de circuito, equivalentes, ejemplos útiles
- CR2032 vs DL2032 vs Guía de comparación CR2025
- Comprensión de las diferencias Análisis técnico y de rendimiento ESP32 y ESP32-S3
- Análisis detallado del circuito de la serie RC
 Análisis en profundidad de 1N4148 Diodos: modos de operación, especificaciones y escenarios de uso
Análisis en profundidad de 1N4148 Diodos: modos de operación, especificaciones y escenarios de uso
2024-05-08
 Comprender los tipos y usos de las bombas de desplazamiento dinámico y positivo
Comprender los tipos y usos de las bombas de desplazamiento dinámico y positivo
2024-05-07
Número de pieza caliente
 CGA3E2C0G2A122J080AD
CGA3E2C0G2A122J080AD 0603YC562K4T2A
0603YC562K4T2A GCM1885C2A4R2CA16D
GCM1885C2A4R2CA16D 1206CC472KAJ1A
1206CC472KAJ1A C1608C0G1H5R6D
C1608C0G1H5R6D F950J686MSAAM1Q
F950J686MSAAM1Q MAX192BEAP+T
MAX192BEAP+T IKCM15L60GAXKMA1
IKCM15L60GAXKMA1 MCP2515T-E/ST
MCP2515T-E/ST LAN9354I/ML
LAN9354I/ML
- MAX516AEWG
- KSZ8873MLLI
- MC145481EGR2
- MTFC2GMDEA-0M WT
- TC4424EOE
- RT0603DRE07100KL
- T491D337M006AT4380
- LTC2606IDD-1#PBF
- T491D336K020ZTPB01
- LM2901VQDRQ1
- LM2833ZSD/NOPB
- XCS10XL-4CS144C
- ADM2582EBRWZ
- XC2C384-10FT256C
- T495B475M025ATE900
- TMS320VC5401ZGU50
- XC5VLX20T-2FFG323C
- ADM1068AST
- BD8655FV-HVE2
- HA17358ATEL-E
- LSISASSG16A1
- MC14081B
- MC74F85DR
- R5F2LA58ANFP
- STMP3410U
- TPC8050-H
- AM79Q021JC
- HM5165165LTT6
- MT46V16M8P-75
- T330N16KOF
- T6UE7XBG-0002W1
- TLV320AIC3212IYZF
- EDD51321CBH-6CTT-E
- MB8666TPMCR-G-BNDE1
- PS8815QFN52GTR-A0
- SSM3J328R.LF
- GK6105SU-D
- C016-20H003-110-12
- LMZ12003TZ-ADJ-NOPB